Остановка 7

От геометрии аналитической
к геометрии проективной

Автостопом по математике

Да-да, мы вернулись к аналитической геометрии.
Собственно, доказательство того факта, что полученное нами при решении системы дифференциальных уравнений из прошлой главы уравнение задает плоскость, было выполнено средствами именно этого отдела математики.

Как вы могли заметить, там мы воспользовались двумя фундаментальными приемами - введением декартовых прямоугольных координат на плоскости и векторной алгеброй

Тем самым, можно показать, что в декартовой прямоугольной системе координат любая прямая определяется уравнением первой степени:

(данное уравнение называют общим уравнением прямой).

Пускай в прямоугольной декартовой системе координат задано уравнение первой степени *******************, где А, В и С – любые числа такие, что А и В одновременно не равны нулю. Пусть, например, *****. Тогда зафиксировав произвольную точку

Значит, существует, по крайней мере, одна точка

удовлетворяющая равенству

Вычитая это равенство из исходного уравнения, получаем

А это есть уравнение прямой, проходящей через точку ********* , перпендикулярно вектору n c координатами (A, B).

Уравнение прямой можно получить и не с помощью перпендикулярного вектора nk, или, как его еще иногда называют – вектора нормали к прямой, а при помощи сонаправленного, или коллинеарного вектора

Фиксируя опять-таки точку *************, отмечаем, что точка ********** будет принадлежать прямой, проходящей через точку **** и параллельной вектору **, если вектор ************************* будет коллинеарен вектору ** т. е. если

Полученное уравнение называют каноническим уравнением прямой. Заметим, что обращение в ноль одного из знаменателей в каноническом уравнении означает обращение в ноль соответствующего числителя.

В самом деле, пропорция

эквивалентна равенству

И если, например, m=0, а n≠0, то это означает, что ************* и мы получаем прямую *******, параллельную оси ординат.

Рассмотрим в заключение снова общее уравнение прямой:

Оно эквивалентно уравнению *************** , или

Обозначив *********** и *********** получим так называемое уравнение прямой в отрезках:

которое названо так потому, что числа a и b – это в точности величины отрезков, которые прямая отсекает на координатных осях, если их откладывать от начала координат:

Видите ли вы, почему это действительно так?

Этими простейшими примерами мы надеялись зародить в вас искренний интерес к тому, как чисто алгебраическими средствами удается определить не только огромный класс линий, но также поверхностей и трехмерных фигур, и – что, возможно, самое интересное – так называемых n-мерных многообразий.

Здесь уместно будет сказать о том, как изменилась роль аналитической геометрии в процессе ее развития.

Изначально казалось совершенно естественным рассматривать точки, кривые и поверхности как чисто геометрические объекты – и применение координатного метода ограничивалось тем, что с его помощью эти самые объекты геометрии удавалось изучать зачастую более удобными алгебраическими или аналитическими методами.

Но затем ситуация изменилась:
Числа, пары чисел, их тройки и т. п. стали рассматриваться как самостоятельные исходные объекты аналитической, вообще говоря, а не геометрической природы – и уже они получали своего рода «геометрические» образы. Эта «геометризация» абстрактных соотношений между теми или иными наборами чисел стала носить вспомогательный, хоть и очень часто продуктивный характер - геометрическая интуиция просто подсказывала наиболее вероятные направления решений уже никак с геометрией не связанных задач.

Так был совершен переход от трех к четырем и большему числу измерений. Наглядность, как будто бы никуда не уходит, даже если мы говорим о «точке» в n-мерном пространстве или о «гиперплоскости» как о совокупности точек *************** , которые удовлетворяют линейному уравнению ********************************** .

Иначе говоря, использование геометрического языка облегчает аналитические рассуждения, а нередко руководит ими и направляет в нужную сторону. Одним из ярчайших примеров является теория относительности, которая объединила три пространственные координаты и одну временную в единое четырехмерное «пространственно – временное» многообразие, называемое, по имени автора его идеи, четырехмерным псевдоевклидовым пространством Минковского.

Обратное тоже верно: любое уравнение первой степени определяет прямую на плоскости. Докажем это.

Доказательство.

Именно геометрическое рассмотрение данной конструкции как неевклидова пространства позволило ответить просто на многие сложные вопросы – такие, в частности, как распространение света по геодезическим линиям в этом «искривленном четырехмерном континууме».

Оказалось, что такие “пространства” и “фигуры” обладают свойствами, которые не зависят от числа измерений, но при этом могут быть наглядно интерпретированы, если их редуцировать к понятному для нас трех- или двумерному случаю.

Выводя уравнение плоскости, мы немного забежали вперед, а могли бы начать и с уравнения прямой линии – алгоритм вывода был бы по сути тем же.

Еще одна пересадочка - в направлении неевклидовых геометрий.

Пересадка.

Через точку на плоскости, не лежащую на данной прямой, нельзя провести ни одной прямой, параллельной данной.

Обе они возникли из отрицания постулата Евклида о параллельных, который можно сформулировать следующим образом: через точку на плоскости, не лежащую на данной прямой, можно провести ровно одну прямую, параллельную данной.

когда речь заходит о Неевклидовой геометрии, то первое, что приходит на ум - это геометрия Римана и геометрия Лобачевского.

Логических отрицаний у этого утверждения может быть два:

Через точку на плоскости, не лежащую на данной прямой, можно провести более одной прямой, параллельной данной.

Добавляя каждое из отрицаний к остальным четырем евклидовым аксиомам, из которых выводится так называемая абсолютная геометрия, мы получаем, соответственно, две неевклидовых – эллиптическую, или Риманову и гиперболическую, или геометрию Лобачевского.

Внимание же тех, кто решил остаться с нами, мы обратим вот на что:

Любые две прямые пересекаются не только в геометрии сферы (на которой прямые – это так называемые линии большого круга, или меридианы, и они, разумеется, всегда пересекаются в полюсах сферы) или в Римановой эллиптической геометрии, но и … в перспективе.

Тот факт, что предметы, расположенные ближе, кажутся крупнее таких же по размеру, но расположенных дальше, был известен человечеству всегда.

Поэтому удивительно, но вплоть до эпохи Возрождения люди не изображали предметы, находящиеся вблизи наблюдателя, бОльшими по размеру, чем те, что находятся от него дальше. Джотто, пожалуй, был первым, кто осознал, что относительные размеры и форма изображений требуют коррекции, чтобы выглядеть более реалистичными. Однако его попытки были несистемными и в большинстве своем ошибочными.

Проблема перспективы, стоявшая перед художниками и архитекторами, в конце концов была ими решена в виде ряда принципов:

eщё два принципа, к которым пришли художники Ренессанса, следующие:

Последний принцип, возможно, труднее всего быстро вообразить, но он тоже вполне естественен, как будет показано ниже.

Принцип утверждает, что при проекции эти кривые могут переходить только друг в друга - например, как в случае, показанном на рисунке, окружность переходит в эллипс:

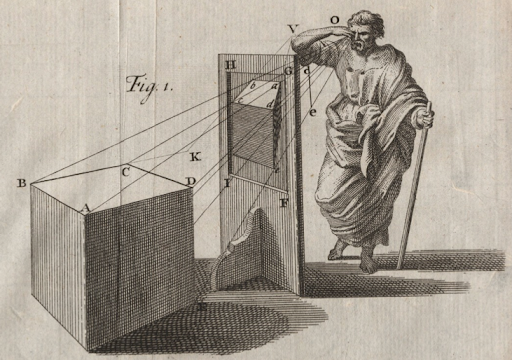
Вообще все принципы проективной геометрии становятся значительно яснее, если мы представим себе, что вообще значит – изобразить тот или иной объемный предмет на плоскости (ну, скажем, холста):

1

2

Всем желающим сойти в этом месте мы рекомендуем продолжить путешествие, освоив в общих чертах Главу «Разные геометрии».

А. Д. Александров, Н. Ю. Нецветаев «Геометрия».
(Глава «Разные геометрии»)

*

С помощью данного принципа удается корректно изобразить, скажем, пол, замощенный квадратной плиткой – используя диагонали, которые тоже параллельны и, следовательно, на изображении должны пересечься в какой-то точке горизонта, можно получать все новые и новые точки пересечения с вертикальными линиями, пересекающимися в другой точке, и таким образом проводить горизонтальные линии на корректных расстояниях друг от друга.

*

Джотто ди Бондоне (1267 - 1337) — Итальянский художник и архитектор, основоположник эпохи Проторенессанса.

Как очень хорошо видно из рисунка, линии, идущие от точек, расположенных близко, составляют с поверхностью Земли, значительные углы.

В данном случае центром проекции (точкой перспективы) является глаз художника, и изображение – это по сути множество точек пересечения линий, идущих от точек объекта и сходящихся в глазу, с плоскостью холста.

Эти углы все больше уменьшаются по мере отдаления точек, и от бесконечно удаленных точек они пойдут в глаз художника параллельно Земле. Точкам пересечения этих линий с плоскостью холста и будет соответствовать линия горизонта на холсте.

Представьте себе параболу y=x2, но только лежащую горизонтально, и себя, стоящих в начале координат и смотрящих в положительном направлении оси Y :

Давайте теперь представим себе нечто чуть более математическое, удерживая в голове тот же образ с глазом.

Согласитесь, что параболу вы не увидите, вы увидите нечто другое - и это нечто снова будет эллипсом! Если еще не согласились, то подумайте, почему будет именно так?

Заметим, что линия горизонта на этом чертеже опять-таки является важной составляющей чертежа – она ему принадлежит. Поэтому часто говорят, что проективная плоскость есть обычная плоскость, к которой добавлена бесконечно удаленная прямая, понимаемая как множество бесконечно удаленных точек, в каждой их которых встречается семейство параллельных прямых каждого из направлений данной плоскости.

К художникам, озабоченным проблемой перспективы, вскоре присоединились геометры – и, в частности, Жерар Дезарг.

Именно он ввел в рассмотрение бесконечно удаленную прямую, и он же по праву считается основателем проективной геометрии – геометрии, которую можно задать по сути всего двумя аксиомами:

Подчеркивая простоту данного вида геометрии, Дезарг называл ее «геометрией одной линейки»

Ну и действительно, тут нет ни координат, ни расстояний ни углов: все, что мы можем делать – так это проводить прямые линии и отмечать точки их пересечения, что создает ощущение удивительной элегантности этого предмета.

Именем Дезарга названа, пожалуй, самая главная теорема проективной геометрии, и на примере данной теоремы как нельзя лучше можно продемонстрировать упомянутые нами простоту и элегантность:

Обратное тоже верно:

Мы сознательно привели столь громоздкую формулировку, чтобы показать, насколько все упрощается, если мы из плоскости опять – таки переместимся в трехмерное пространство:

Для любых двух точек плоскости существует ровно одна прямая, проходящая через эти две точки

Для любых двух прямых плоскости существует ровно одна точка, в которой эти две прямые пересекаются

1

2

(geometry of straightedge).

В этом случае теорема попросту утверждает, что два треугольника имеют общую точку перспективы в том и только в том случае, когда они имеют общую линию перспективы.

Если пока не очевидно, то давайте рассмотрим фрагмент этой же проекции и то, как она строится:

И последнее утверждение в совокупности с картинкой практически очевидно, не правда ли?

Предположим, мы проецируем с плоскости ** на плоскость ** сторону АВ треугольника АВС. Как мы должны изобразить на плоскости ** образ прямой, проходящей через точки А и В.

Это становится понятным, если мы заметим, что один конец прямой должен уйти на бесконечность и будет соответствовать некоторой точке на линии горизонта, а второй конец как раз пересечется с линией перспективы в некоторой точке М, и эта точка будет являться неподвижной точкой для данного проективного преобразования:

Соответственно, для корректного построения проекции прямой АВ и нахождения местоположения точек A' и B' нам необходима бесконечно удаленная линия горизонта и точка N на плоскости λ', соответствующая образу бесконечно удаленной точки прямой АВ на плоскости λ.

Помните, семейство параллельных прямых каждого направления пересекает горизонт в своей точке?

Ее мы, таким образом, находим, проводя из точки проекции прямую, параллельную прямой АВ. Значит, по построению, образ прямой АВ есть прямая MN, где точка М – неподвижная точка преобразования проектирования. Поскольку рассуждения для оставшихся двух сторон тождественны только что проведенному, то «продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой» l просто по построению проективного отображения.

Удалось ли вам разделить вместе с Жераром Дезаргом лаконичную красоту проективной геометрии?

А ведь это самое ее начало. Впереди вас ждут однородные координаты, проективные пространства и подчас далеко не очевидные инварианты проективных преобразований...

Системное и последовательное знакомство с этой поистине удивительной геометрией мы рекомендуем вам начать с книги Вольберга “Основные идеи проективной геометрии”.

Впереди вас ждут однородные координаты, проективные пространства и подчас далеко не очевидные инварианты проективных преобразований...

О. А. Вольберг
«Основные идеи проективной геометрии»

Существует также классический учебник Хартсхорна “Основы проективной геометрии”, но он гораздо более сухо написан. В любом случае - выбор за вами.

Р. Хартсхорн
«ОСновы проективной геометрии»

Ну вот и подошло к концу наше с вами небольшое путешествие по пространству математического.

Мы далеки от иллюзии, что обошли все - по пути мы проходили пересадки и развилки, путь по которым также может для кого то составить смысл всей жизни. Но мы все же надеемся, что нам удалось побыть для вас проводником в той самодостаточной Вселенной, какой является математика - а присутствие проводника всегда хоть немного, да успокаивает.

Надеемся также, что наша роль не сводилась к пустышке - плацебо, и те темы, мимо которых и по которым мы проходили, стали для вас яснее и притягательнее.

Мы не прощаемся, и обещаем, что совсем скоро предложим вам новые, столь же увлекательные и, одновременно, столь же безопасные маршруты.
До новых встреч!